CHAPTER XII – Space and Counter-Space
PART II: Goetheanism – Whence and Whither?
CHAPTER XII Space and Counter-Space
With the introduction, in Chapter X, of the peripheral type of force-field which appertains to levity as the usual central one does to gravity, we are compelled to revise our conception of space. For in a space of a kind we are accustomed to conceive, that is, the three-dimensional, Euclidean space, the existence of such a field with its characteristic of increasing in strength in the outward direction is a paradox, contrary to mathematical logic.
This task, which in view of our further observations of the actions of the levity-gravity polarity in nature we must now tackle, is, however, by no means insoluble. For in modern mathematics thought-forms are already present which make it possible to develop a space-concept adequate to levity. As referred to in Chapter I, it was Rudolf Steiner who first pointed to the significance in this respect of the branch of modern mathematics known as Projective Geometry. He showed that Projective Geometry, if rightly used, carries over the mind from the customary abstract to a new concrete treatment of mathematical concepts. The following example will serve to explain, to start with, what we mean by saying that mathematics has hitherto been used abstractly.
One of the reasons why the world-picture developed by Einstein in his Theory of Relativity deserves to be acknowledged as a step forward in comparison with the picture drawn by classical physics, lies in the fact that the old conception of three-dimensional space as a kind of ‘cosmic container’, extending in all directions into infinity and filled, as it were, with the content of the physical universe, is replaced by a conception in which the structure of space results from the laws interrelating this content. Our further discussion will show that this indeed is the way along which, to-day, mathematical thought must move in order to cope with universal reality.
However, for reasons discussed earlier, Einstein was forced to conceive all events in the universe after the model of gravity as observable on the earth. In this way he arrived at a space-structure which possesses neither the three-dimensionality nor the rectilinear character of so-called Euclidean space – a space-picture which, though mathematically consistent, is incomprehensible by the human mind. For nothing exists in our mind that could enable us to experience as a reality a space-time continuum of three dimensions which is curved within a further dimension.
This outcome of Einstein’s endeavours results from the fact that he tried by means of gravity-bound thought to comprehend universal happenings of which the true causes are non-gravitational. A thinking that has learnt to acknowledge the existence of levity must indeed pursue precisely the opposite direction. Instead of freezing time down into spatial dimension, in order to make it fit into a world ruled by nothing but gravity, we must develop a conception of space sufficiently fluid to let true time have its place therein. We shall see how such a procedure will lead us to a space-concept thoroughly conceivable by human common sense, provided we are prepared to overcome the onlooker-standpoint in mathematics also.
Einstein owed the possibility of establishing his space-picture to a certain achievement of mathematical thinking in modern times. As we have seen, one of the peculiarities of the onlooker-consciousness consists in its being devoid of all connexion with reality. The process of thinking thereby gained a degree of freedom which did not exist in former ages. In consequence, mathematicians were enabled in the course of the nineteenth century to conceive the most varied space-systems which were all mathematically consistent and yet lacked all relation to external existence. A considerable number of space-systems have thus become established among which there is the system that served Einstein to derive his space-time concept. Some of them have been more or less fully worked out, while in certain instances all that has been done is to show that they are mathematically conceivable. Among these there is one which in all its characteristics is polarically opposite to the Euclidean system, and which is destined for this reason to become the space-system of levity. It is symptomatic of the remoteness from reality of mathematical thinking in the onlooker-age that precisely this system has so far received no special attention.1
For the purpose of this book it is not necessary to expound in detail why modern mathematical thinking has been led to look for thought-forms other than those of classical geometry. It is enough to remark that for quite a long time there had been an awareness of the fact that the consistency of Euclid’s definitions and proofs fails as soon as one has no longer to do with finite geometrical entities, but with figures which extend into infinity, as for instance when the properties of parallel straight lines come into question. For the concept of infinity was foreign to classical geometrical thinking. Problems of the kind which had defeated Euclidean thinking became soluble directly human thinking was able to handle the concept of infinity.
We shall now indicate some of the lines of geometrical thought which follow from this.
*
Let us consider a straight line extending without limits in either direction. Projective geometry is able to state that a point moving along this line in one direction will eventually return from the other. To see this, we imagine two straight lines a and b intersecting at P. One of these lines is fixed (a); the other (b) rotates uniformly about C. Fig. 7 indicates the rotation of b by showing it in a number of positions with the respective positions of its point of intersection with a (P1, P2. . .). We observe this point moving along a, as a result of the rotation of b, until, when both lines are parallel, it reaches infinity. As a result of the continued rotation of b, however, P does not remain in infinity, but returns along a from the other side. We find here two forms of movement linked together – the rotational movement of a line (b) on a point (C), and the progressive movement of a point (P) along a line (a). The first movement is continuous, and observable throughout within finite space. Therefore the second movement must be continuous as well, even though it partly escapes our observation. Hence, when P disappears into infinity on one side of our own point of observation, it is at the same time in infinity on the other side. In order words, an unlimited straight line has only one point at infinity.
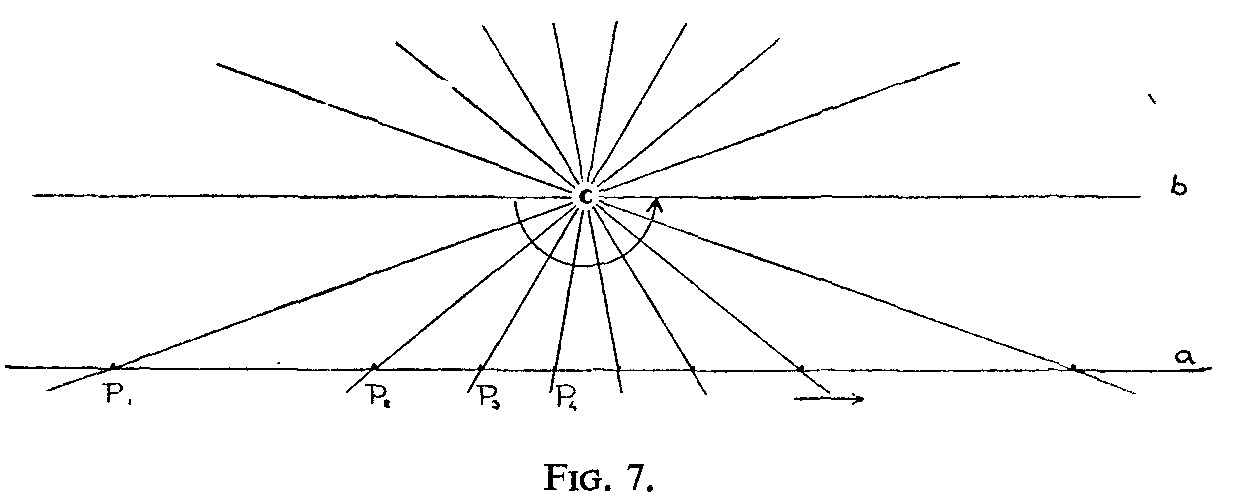It is clear that, in order to become familiar with this aspect of geometry, one must grow together in inward activity with the happening which is contained in the above description. What we therefore intend by giving such a description is to provide an opportunity for a particular mental exercise, just as when we introduced Goethe’s botany by describing a number of successive leaf-formations. Here, as much as there, it is the act of ‘re-creating’ that matters.
The following exercise will help us towards further clarity concerning the nature of geometrical infinity.
We imagine ourselves in the centre of a sphere which we allow to expand uniformly on all sides. Whilst the inner wall of this sphere withdraws from us into ever greater distances, it grows flatter and flatter until, on reaching infinite distance, it turns into a plane. We thus find ourselves surrounded everywhere by a surface which, in the strict mathematical sense, is a plane, and is yet one and the same surface on all sides. This leads us to the conception of the plane at infinity as a self-contained entity although it expands infinitely in all directions.
This property of a plane at infinity, however, is really a property of any plane. To realize this, we must widen our conception of infinity by freeing it from a certain one-sidedness still connected with it. This we do by transferring ourselves into the infinite plane and envisaging, not the plane from the point, but the point from the plane. This operation, however, implies something which is not obvious to a mind accustomed to the ordinary ways of mathematical reasoning. It therefore requires special explanation.
In the sense of Euclidean geometry, a plane is the sum-total of innumerable single points. To take up a position in a plane, therefore, means to imagine oneself at one point of the plane, with the latter extending around in all directions to infinity. Hence the journey from any point in space to a plane is along a straight line from one point to another. In the case of the plane being at infinity, it would be a journey along a radius of the infinitely large sphere from its centre to a point at its circumference.
In projective geometry the operation is of a different character. Just as we arrived at the infinitely large sphere by letting a finite sphere grow, so must we consider any finite sphere as having grown from a sphere with infinitely small extension; that is, from a point. To travel from the point to the infinitely distant plane in the sense of projective geometry, therefore, means that we have first to identify ourselves with the point and ‘become’ the plane by a process of uniform expansion in all directions.
As a result of this we do not arrive at one point in the plane, with the latter extending round us on all sides, but we are present in the plane as a whole everywhere. No point in it can be characterized as having any distance, whether finite or infinite, from us. Nor is there any sense in speaking of the plane itself as being at infinity. For any plane will allow us to identify ourselves with it in this way. And any such plane can be given the character of a plane at infinity by relating it to a point infinitely far away from it (i.e. from us).
Having thus dropped the one-sided conception of infinity, we must look for another characterization of the relationship between a point and a plane which are infinitely distant from one another. This requires, first of all, a proper characterization of Point and Plane in themselves.
Conceived dynamically, as projective geometry requires, Point and Plane represent a pair of opposites, the Point standing for utmost contraction, the Plane for utmost expansion. As such, they form a polarity of the first order. Both together constitute Space. Which sort of space this is, depends on the relationship in which they are envisaged. By positing the point as the unit from which to start, and deriving our conception of the plane from the point, we constitute Euclidean space. By starting in the manner described above, with the plane as the unit, and conceiving the point from it, we constitute polar-Euclidean space.
The realization of the reversibility of the relationship between Point and Plane leads to a conception of Space still free from any specific character. By G. Adams this space has been appositely called archetypal space, or ur-space. Both Euclidean and polar-Euclidean space are particular manifestations of it, their mutual relationship being one of metamorphosis in the Goethean sense.
Through conceiving Euclidean and polar-Euclidean space in this manner it becomes clear that they are nothing else than the geometrical expression of the relationship between gravity and levity. For gravity, through its field spreading outward from an inner centre, establishes a point-to-point relation between all things under its sway; whereas levity draws all things within its domain into common plane-relations by establishing field-conditions wherein action takes place from the periphery towards the centre. What distinguishes in both cases the plane at infinity from all other planes may be best described by calling it the all-embracing plane; correspondingly the point at infinity may be best described as the all-relating point.
In outer nature the all-embracing plane is as much the ‘centre’ of the earth’s field of levity as the all-relating point is the centre of her field of gravity. All actions of dynamic entities, such as that of the ur-plant and its subordinate types, start from this plane. Seeds, eye-formations, etc., are nothing but individual all-relating points in respect of this plane. All that springs from such points does so because of the point’s relation to the all-embracing plane. This may suffice to show how realistic are the mathematical concepts which we have here tried to build up.
*
When we set out earlier in this book (Chapter VIII) to discover the source of Galileo’s intuition, by which he had been enabled to find the theorem of the parallelogram of forces, we were led to certain experiences through which all men go in early childhood by erecting their body and learning to walk. We were thereby led to realize that man’s general capacity for thinking mathematically is the outcome of early experiences of this kind. It is evident that geometrical concepts arising in man’s mind in this way must be those of Euclidean geometry. For they are acquired by the will’s struggle with gravity. The dynamic law discovered in this way by Galileo was therefore bound to apply to the behaviour of mechanical forces – that is, of forces acting from points outward.
In a similar way we can now seek to find the source of our capacity to form polar-Euclidean concepts. As we were formerly led to experiences of man’s early life on earth, so we are now led to his embryonic and even pre-embryonic existence.
Before man’s supersensible part enters into a physical body there is no means of conveying to it experiences other than those of levity, and this condition prevails right through embryonic development. For while the body floats in the mother’s foetal fluid it is virtually exempt from the influence of the earth’s field of gravity.
History has given us a source of information from these early periods of man’s existence in Traherne’s recollections of the time when his soul was still in the state of cosmic consciousness. Among his descriptions we may therefore expect to find a picture of levity-space which will confirm through immediate experience what we have arrived at along the lines of realistic mathematical reasoning. Among poems quoted earlier, his The Praeparative and My Spirit do indeed convey this picture in the clearest possible way. The following are relevant passages from these two poems.
In the first we read:
‘Then was my Soul my only All to me,
A living endless Ey,
Scarce bounded with the Sky
Whose Power, and Act, and Essence was to see:
I was an inward Sphere of Light,
Or an interminable Orb of Sight,
Exceeding that which makes the Days . . .’
In the second poem the same experience is expressed in richer detail. There he says of his own soul that it –
… being Simple, like the Deity,
In its own Centre is a Sphere,
Not limited but everywhere.
It acts not from a Centre to
Its Object, as remote;
But present is, where it doth go
To view the Being it doth note …
A strange extended Orb of Joy
Proceeding from within,
Which did on ev’ry side display
Its force; and being nigh of Kin
To God, did ev’ry way
Dilate its Self ev’n instantaneously,
Yet an Indivisible Centre stay,
In it surrounding all Eternity.
‘Twas not a Sphere;
Yet did appear
One infinite: ‘Twas somewhat everywhere.’
Observe the distinct description of how the relation between circumference and centre is inverted by the former becoming itself an ‘indivisible centre’. In a space of this kind there is no Here and There, as in Euclidean space, for the consciousness is always and immediately at one with the whole space. Motion is thus quite different from what it is in Euclidean space. Traherne himself italicized the word ‘instantaneous’, so important did he find this fact. (The quality of instantaneousness – equal from the physical point of view to a velocity of the value âž – will occupy us more closely as a characteristic of the realm of levity when we come to discuss the apparent velocity of light in connexion with our optical studies.)
By thus realizing the source in man of the polar-Euclidean thought-forms, we see the discovery of projective geometry in a new light. For it now assumes the significance of yet another historical symptom of the modern re-awakening of man’s capacity to remember his prenatal existence.
We know from our previous studies that the concept of polarity is not exhausted by conceiving the world as being constituted by polarities of one order only. Besides primary polarities, there are secondary ones, the outcome of interaction between the primary poles. Having conceived of Point and Plane as a geometrical polarity of the first order, we have therefore to ask what formative elements there are in geometry which represent the corresponding polarity of the second order. The following considerations will show that these are the radius, which arises from the point becoming related to the plane, and the spherically bent surface (for which we have no other name than that again of the sphere), arising from the plane becoming related to the point.
In Euclidean geometry the sphere is defined as ‘the locus of all points which are equidistant from a given point’. To define the sphere in this way is in accord with our post-natal, gravity-bound consciousness. For in this state our mind can do no more than envisage the surface of the sphere point by point from its centre and recognize the equal distance of all these points from the centre. Seen thus, the sphere arises as the sum-total of the end-points of all the straight lines of equal length which emerge from the centre-point in all directions. Fig. 8 indicates this schematically. Here the radius, a straight line, is clearly the determining factor.
We now move to the other pole of the primary polarity, that is to the plane, and let the sphere arise by imagining the plane approaching an infinitely distant point evenly from all sides. We view the process realistically only by imagining ourselves in the plane, so that we surround the point from all sides, with the distance between us and the point diminishing gradually. Since we remain all the time on the surface, we have no reason to conceive any change in its original position; that is, we continue to think of it as an all-embracing plane with regard to the chosen point.
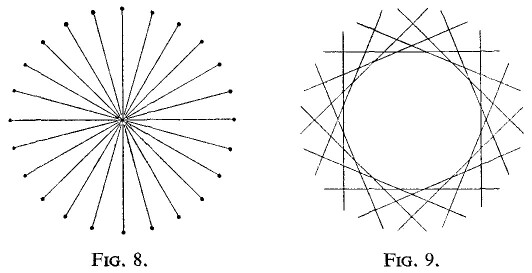The only way of representing the sphere diagrammatically, as a unit bearing in itself the character of the plane whence it sprang, is as shown in Fig. 9, where a number of planes, functioning as tangential planes, are so related that together they form a surface which possesses everywhere the same distance from the all-relating point.
Since Point and Plane represent in the realm of geometrical concepts what in outer nature we find in the form of the gravity-levity polarity, we may expect to meet Radius and Sphere as actual formative elements in nature, wherever gravity and levity interact in one way or another. A few observations may suffice to give the necessary evidence. Further confirmation will be furnished by the ensuing chapters.
The Radius-Sphere antithesis appears most obviously in the human body, the radial element being represented by the limbs, the spherical by the skull. The limbs thus become the hieroglyph of a dynamic directed from the Point to the Plane, and the skull of the opposite. This indeed is in accord with the distribution in the organism of the sulphur-salt polarity, as we learnt from our physiological and psychological studies. Inner processes and outer form thus reveal the same distribution of poles.
In the plant the same polarity appears in stalk and leaf. Obviously the stalk represents the radial pole. The connexion between leaf and sphere is not so clear: in order to recognize it we must appreciate that the single plant is not a self-contained entity to the same degree as is the human being. The equivalent of the single man is the entire vegetable covering of the earth. In man there is an individual centre round which the bones of his skull are curved; in the plant world the equivalent is the centre of the earth. It is in relation to this that we must conceive of the single leaves as parts of a greater sphere.
In the plant, just as in man, the morphological polarity coincides with the biological. There is, on the one hand, the process of assimilation (photosynthesis), so characteristic of the leaf. Through this process matter passes over from the aeriform condition into that of numerous separate, characteristically structured solid bodies – the starch grains. Besides this kind of assimilation we have learnt to recognize a higher form which we called ‘spiritual assimilation’. Here, a transition of substance from the domain of levity to that of gravity takes place even more strikingly than in ordinary (physical) assimilation (Chapter X).
The corresponding process in the linear stalk is one which we may call ‘sublimation’ – again with its extension into ‘spiritual sublimation’. Through this process matter is carried in the upward direction towards ever less ponderable conditions, and finally into the formless state of pure ‘chaos’. By this means the seed is prepared (as we have seen) with the help of the fire-bearing pollen, so that after it has fallen to the ground, it may serve as an all-relating point to which the plant’s Type can direct its activity from the universal circumference.
In order to find the corresponding morphological polarity in the animal kingdom, we must realize that the animal, by having the main axis of its body in the horizontal direction, has a relationship to the gravity-levity fields of the earth different from those of both man and plant. As a result, the single animal body shows the sphere-radius polarity much less sharply. If we compare the different groups of the animal kingdom, however, we find that the animals, too, bear this polarity as a formative element. The birds represent the spherical (dry, saline) pole; the ruminants the linear (moist, sulphurous) pole. The carnivorous quadrupeds form the intermediary (mercurial) group. As ur-phenomenal types we may name among the birds the eagle, clothed in its dry, silicic plumage, hovering with far-spread wings in the heights of the atmosphere, united with the expanses of space through its far-reaching sight; among the ruminants, the cow, lying heavily on the ground of the earth, given over entirely to the immensely elaborated sulphurous process of its own digestion. Between them comes the lion – the most characteristic animal for the preponderance of heart-and-lung activities in the body, with all the attributes resulting from that.
Within the scope of this book it can only be intimated briefly, but should not be left unmentioned for the sake of those interested in a further pursuit of these lines of thought, that the morphological mean between radius and sphere (corresponding to Mercurius in the alchemical triad) is represented by a geometrical figure known as the ‘lemniscate’, a particular modification of the so-called Cassinian curves.2
1 For further details, see the writings of G. Adams and L. Locher-Ernst who, each in his own way, have made a beginning with applying projective geometry on the lines indicated by Rudolf Steiner. Professor Locher-Ernst was the first to apply the term ‘polar-Euclidean’ to the space-system corresponding to levity.
2 For particulars of the lemniscate as the building plan of the middle part of man’s skeleton, see K. König, M.D.: Beitrage zu einer reinen Anatomic des menschlichen Knochenskeletts in the periodical Natura (Dornach, 1930-1). Some projective-geometrical considerations concerning the lemniscate are to be found in the previously mentioned writings of G. Adams and L. Locher-Ernst.